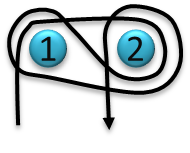There’s a somewhat well-known problem called the “Picture Hanging Problem.” The story goes:
Suppose your roommate asked you to hang an ugly painting on the wall, while he leaves to do some errands. You don’t want to hurt your roommate’s feelings by saying it’s ugly and you don’t want to be responsible for breaking it yourself, but you also don’t want it to be hung up, because of how ugly it is. While your roommate is gone, you come up with an ingenious strategy: you will hang the picture up by two nails, knowing that your roommate will remove one of them (because of how inefficient two nails is). Of course, when he removes this nail, you want the picture to fall and break. Thus, the picture will not stay up, and you won’t be responsible.
Find some way to hang a picture (with the arbitrarily long, infinitely light and thin string already on) on two nails, spaced apart horizontally to the ground, so that when either nail is removed, the picture will fall.
This problem is really interesting in that it can be extended to much more general cases. Solve the Picture Hanging problem for:
- $2$ nails, pulling any $1$ out, as described above.
- $3$ nails, pulling any $2$ out.
- $N$ nails, pulling any $N-1$ out.
- $3$ nails, pulling any $1$ out.
- $4$ nails, pulling any $1$ out.
- $4$ nails, pulling any $2$ out.
- $N$ nails, pulling any $1$ out.
- $N$ nails, pulling any $k$, $1 \le k < N$ out.
What is the minimum number “wraps” needed to accomplish each of the above statements, where a wrap is some amount of a turn around a nail?
show
Without using mathematics that are too complex, we can equate this problem to one of grouping matrices and inverse matrices. Let’s let $p_k$ represent a clockwise “wrap” around nail $p$, and $p’_k$ represent a counterclockwise wrap around nail $k$, in other words, the inverse of $p_k$. Then we can notice several things.
For now, let’s consider nails $1$ and $2$. Notice that $p_1 p_2$ which means a CW wrap around nail $1$ followed by a CW wrap around nail $2$ is not the same as $p_2 p_1$. Notice that $p_1 p’_1$ = $1$, in other words, they cancel. But also notice that in $p_1 p_2 p’_1$, the $p_1$ components don’t cancel, because of the $p_2$ component in between. So already we see properties of commuting and inverses. With these in mind, consider a few illustrated cases:
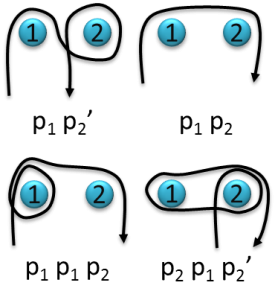
Picture Hanging Notation Examples
With this mindset, solving the picture hanging problems is a lot easier; we can do this using a sort of educated guess and check.
- $p_1 p_2 p’_1 p’_2$
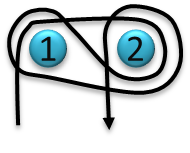
Picture Hanging $2$-nail Solution
- $p_1 p_2 p_3 p’_1 p’_2 p’_3$
- $p_1 p_2 \cdots p_N p’_1 p’_2 \cdots p’_N$
- $p_1 p_2 p_3 p’_2 p’_3 p’_1 p_3 p_2 p’_3 p’_2$
- $p_1 p_2 p’_1 p’_2 p_3 p_4 p’_3 p’_4 p_2 p_1 p’_2 p’_1 p_4 p_3 p’_4 p’_3$
- $p_1 p_2 p_3 p’_1 p’_2 p’_3 p_2 p_3 p_4 p’_2 p’_3 p’_4 p_3 p_2 p_1 p’_3 p’_2 p’_1 p_4 p_3 p_2 p’_4 p’_3 p’_2$
(Note: This is not the shortest number of wraps needed.)
-
We can use a recursive process. Starting from $p_1 p_2 p’_1 p’_2$, replace the least populace nail $p_i$ with the form $p_i p_j p’_i p’_j$, $(p_i p_j p’_i p’_j)’ = p_j p_i p’_j p’_i$ where $p_j$ is the nail to add.
Without proof, assume this method yields the shortest chain of wraps for the “N-nail choose $1$” problem. Then we can also see that the N-nail choose $1$ problem will require the number of nails given by this sequence: A073121 (why?)
- $N$ nails, pulling any $k$, $1 \le k < N$ out: I’ll leave this as an exercise to the reader. 😉