Here’s another interesting problem I received from one of my friends:
A Prison Warden is facing an overcrowding problem in his prison. Specifically, there are $N$ prisoners and he wants to play a game with them to reduce the overcrowding problem.
The game works as follows: the Warden will set up $N$ urns and place slips of paper with the prisoners’ $N$ unique names one per urn. Then he’ll bring one prisoner in at a time and let him look at up to $\frac{N}{2}$ urns sequentially, trying to find his name. If he finds his name, the warden will bring in the next prisoner. If he doesn’t find his name, the warden will execute all of the prisoners. The warden will explain the rules of the game to the prisoners and allow them to converse on a strategy, but after that, they are all separated and are thereafter not allowed to communicate with each other.
A naïve strategy is to have all $N$ prisoners look randomly at urns. However, this strategy would give the prisoners a survival rate of $\frac{1}{2^N}$. In a standard case of $N=100$, this gives a survival rate of about $7.89 \cdot 10^{-29} \%$… Not a good rate of survival at all.
Given that there are $N$ prisoners, and that each prisoner plays optimally:
- What is the optimal strategy the prisoners can use for survival?
- What would the expected survival rate be?
show
It turns out you can get about $31 \%$ survival rate for $N = 100$ prisoners. In order to achieve this, we need to take advantage of the fact that the placement of urns doesn’t change from prisoner to prisoner, and the fact that they can collaborate before the game starts.
One idea that might pop up is to create a mapping from names to urns. Then we could look at one urn, find the name in it, and go to the urn that that name “points” to. To illustrate, consider 9 prisoners: A, B, C, …, I. Let’s say “A” maps to $1$, “B” to $2$, etc. Then we’d have paths that look like as follows:
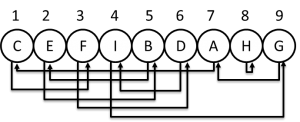
Prisoners and Urns Example ($N = 9$)
But we can notice that there are cycles. And a little thought reveals why every element has to belong to a cycle – since we’ve made a 1-1 mapping, only one name can map to a given urn, so every urn must be mapped to and every urn maps to another urn, thus necessitating every element to be in a cycle.
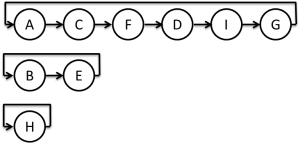
Prisoners and Urns Cycles
Now, it’s fairly obvious what we need to do. We need each prisoner to pick the cycle that contains his/her urn. To guarantee this, we simply pick the urn that is mapped to by that prisoner’s name. For example, prisoner “E” will start by looking at urn $5$. From the diagram above, it’s clear that he will find his name after looking at two urns.
OK, so we have a method of prisoners finding names, but why is that useful? Well, since the cycles can be smaller than or equal to $\frac{N}{2}$ in length, a fortuitous choice of mappings will yield a system in which ALL cycles are less than $\frac{N}{2}$ in length, in which case, all prisoners will survive. In the case above, the prisoners will not survive, but as it turns out, a random choice of mapping will yield survival in around $31 \%$ of cases for $N = 100$.
It’s a bit harder to figure out the probability of survival for $N$ prisoners. This probability is (from Wikipedia):
$$1 – \sum\limits_{k = n+1}^{2n} \frac{1}{k}$$
An interesting result is that we can see as $N \rightarrow \infty$, the probability approaches $1 – \log 2 \approx 30.7 \%$. In other words, for any $N$, the probability of survival is greater than $\approx 30.7 \%$.

