Infinite Power Towers
Power towers take the form $a^{b^{c^{\iddots}}}$ and are evaluated as $a^{(b^{(c^{(\iddots)})})}$. In this way, $3^{3^{3}} = 3^{27} = 7.62559748 \times 10^{12}$.
Infinite power towers simply iterate an exponential operation infinitely. We could define some function $P(a)$ which does this: $P(a) = a^{a^{a^{\iddots}}}$, as shown in the problem statement. For me, it’s not very clear that this should converge on values of $a$ greater than $1$.
Initial Problem Analysis
Suppose $P(a)$ does converge. We can see that if it does converge, then $P(a) = a^{P(a)}$ by the iterative process of power tower exponentiation described above. OK, so how do we solve for $P(a)$?
Let’s set $P(a) = x$ for simplicity. Then we want to solve for $x$ in $a^x = x$.
$$
\begin{eqnarray}
a^x & = & x \\
1 & = & x a^{-x} \\
1 & = & x e^{-x \log{a}} \\
-\log{a} & = & -x \log(a) e^{-x \log{a}} \\
-x \log{a} & = & W(-\log{a}) \\
x & = & \frac{W(-\log{a})}{-\log{a}}
\end{eqnarray}
$$
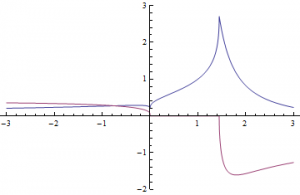
Where $W(x)$ is the Product Log function (more on this later). As a spoiler, here’s a graph of $P(a) = x$ as a function of $a$ (blue line is the real part, red line is the imaginary part). Obviously, the answer shouldn’t be complex, so we can already see the approximate domain of $P(a)$.
Clearly, $a$ is restricted by the constraints of the domain of $\frac{W(-\log{a})}{-\log{a}}$. (Obviously, $a > 0$). Additionally, $a$ is probably constrained by some upper bound, $k$. If this is so, then $k$ would be the value of interest to solve the second question I posed. Note that $\log{a}$ is defined for $a > 0$, so we really just need to find the domain of $W$.
Product Log Function
Wikipedia actually has a nice discussion on this function: Product_Log. Essentially, it can be defined as follows. Suppose $f(x) = x e^x$, then the Product Log function is simply the inverse of $f(x)$ – it finds the value of $x$ for a given $f(x)$. $W(f(x)) = x$. This is why, in the earlier analysis, we could solve for $-x \log(a)$ in $-\log{a} = -x \log(a) e^{-x \log{a}}$.
Note: $W(x)$ is actually dual-valued for some values of $x$. When I use $W(x)$, I’ll be referring to $W_0(x)$, or the upper branch of the Product Log function.
To find the domain of $W$, I’ll use a sort of cheap trick that probably won’t always work, but in this case it does. Basically, I’ll find the Taylor expansion of $W(x)$ around $0$ and find the radius of convergence. While this method does yield the correct result in this case, there’s probably some better way to do it.
Taylor Expansion of the Product Log Function
To find the Taylor Expansion, we can use the Lagrange Inversion Theorem that gives the Taylor Expansion for the inverse of a function.
$$
\begin{eqnarray}
W(z) & = & a + \sum\limits_{n=1}^{\infty} \left( \lim\limits_{x \rightarrow a} \left( \frac{d^{n-1}}{dx^{n-1}} \left( \frac{x-a}{f(x)-b} \right)^n \right) \frac{(z-b)^n}{n!} \right) \\
& = & \sum\limits_{n=1}^{\infty} \left( \lim\limits_{x \rightarrow 0} \left( \frac{d^{n-1}}{dx^{n-1}} \left( \frac{x}{x e^x} \right)^n \right) \frac{(z)^n}{n!} \right) \\
& = & \sum\limits_{n=1}^{\infty} \left( \lim\limits_{x \rightarrow 0} \left( \frac{d^{n-1}}{dx^{n-1}} e^{-nx} \right) \frac{(z)^n}{n!} \right) \\
& = & \sum\limits_{n=1}^{\infty} \left( \lim\limits_{x \rightarrow 0} (-n)^{n-1} e^{-nx} \frac{(z)^n}{n!} \right) \\
& = & \sum\limits_{n=1}^{\infty} \left( \frac{(-n)^{n-1}}{n!} z^n \right)
\end{eqnarray}
$$
Ratio Test of the Product Log Function
To test the radius of convergence of the Taylor Series found above, we can just use the ratio test. We’ll set the absolute value of the ratio of the $(n+1)^{\text{th}}$ term to the $n^{\text{th}}$ term to $1$ and solve for $z$, as $n$ approaches infinity.
$$
\begin{eqnarray}
1 & = & \lim\limits_{n \rightarrow \infty} \left| \frac{\frac{(-(n+1))^{(n+1)-1}}{(n+1)!}z^{n+1}}{\frac{(-n)^{n-1}}{n!}z^n} \right| \\
& = & \lim\limits_{n \rightarrow \infty} \frac{(n+1)^n n!}{n^{n-1} (n+1)!} z \\
& = & \lim\limits_{n \rightarrow \infty} \frac{(n+1)^{n-1}}{n^{n-1}} z \\
& = & \lim\limits_{n \rightarrow \infty} \left(1+\frac{1}{n} \right)^{n-1} z \\
& = & z e
\end{eqnarray}
$$
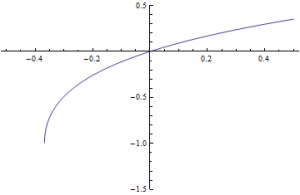
Thus, $z = \frac{1}{e} = $ radius of convergence. This suggests that the product log is not defined below $-\frac{1}{e}$. We can see that it is defined at $-\frac{1}{e}$ (and is $-1$) because $-1 e^{-1} = -\frac{1}{e}$. Here’s a graph of the Product Log function which agrees with this analysis:
Final Analysis
We assume that the argument to $W(x)$ must be greater than or equal to $-\frac{1}{e}$.
$$
\begin{eqnarray}
-\log{a} & \ge & -\frac{1}{e} \\
\log{a} &\le & \frac{1}{e} \\
a & \le & e^{\frac{1}{e}}
\end{eqnarray}
$$
Thus, we find that $k = e^{\frac{1}{e}}$. Furthermore, some of the values of $a$ which satisfy a convergent infinite power tower: $(0 < a \le e^{\frac{1}{e}})$, although there are other special values of $a$ that work, such as $a = -1$. I have left out a lot of analysis as to why it works for values of $a$ between $0$ and $e^{e^{-1}}$, non-inclusive, but I think that's all the time I have now for analysis of this interesting function. Also of interest: What value does $a^{a^{a^{\iddots}}}$ converge to for $a = e^{e^{-1}}$? Recall that: $$ \begin{eqnarray} x & = & \frac{W(-\log{a})}{-\log{a}} \\ & = & \frac{W(-\log{e^{e^{-1}}})}{-\log{e^{e^{-1}}}} \\ & = & \frac{W(-e^{-1})}{-e^{-1}} \\ & = & \frac{-1}{-e^{-1}} \\ & = & e \end{eqnarray} $$ Well isn't that nice? So the maximum value of $a$ for which $a^{a^{a^{\iddots}}}$ converges is $a = e^{e^{-1}}$, and the value it converges to is simply $e$. Final note: Eisenstein apparently did a large amount of analysis on infinite power towers in 1844. More information can be found here.