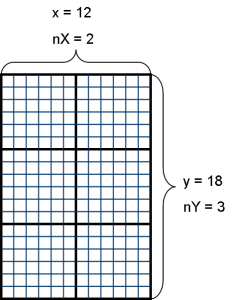What follows is an edited portion of my final research paper (what I consider to be general information everyone knows). While it doesn’t even begin to describe the goals of my research, it should give a good idea about what I did.
Benchmarking Parallel Frameworks for Performance and Ease of Use
Parallel Processing
Most modern programs are serial, meaning that one process executes the code at any time. For some programs, this is necessary, as to get from one step to the next requires results from the previous step. However, many applications rely on performing many identical tasks over a large computational domain for many iterations. This begs the use of parallel processors, which can each take a small portion of the computational domain to work on. Theoretically, $N$ processors could solve a highly parallel problem in $\frac{1}{N}$ time. There are two major types of parallel processing – shared memory and distributed memory.
In a shared memory system, there is one global memory and many processors which can each access different parts of the memory to perform computation. The main advantage of this system is that it’s fairly simple to code and has no need for message passing – each process can read from the main memory. The major disadvantages of this system are that memory accesses and writes have to be done carefully so that multiple processors don’t change a cell at the same time. Additionally, this method can be slow because each process has to access memory stored in a remote location and memory concentration at that location is increased.
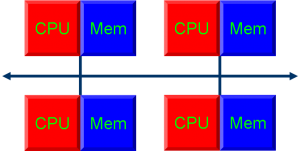
In a distributed memory system, each processor has access to only a local portion of the global array. This means that if computations on one cell require seeing the value of neighbor cells, these neighbor values will have to be passed in as messages from the neighboring processes. See below for a 4-processor system example. Distributed memory systems are useful in that each process has access to its own local memory, so changing these values is as simple as modifying a normal array (no need to check if another process is trying to access the same location). Memory access is also fast because it is stored locally. Distributed memory systems can be more difficult to code since the program usually has to deal with message passing from and two neighboring processes.
Distributing Arrays Across Multiple Processes
To create parallel code in MPI (a distributed memory system) you have to decomposition the domain amongst the $N$ processors. In one dimension, this is trivial. However, most applications rely on a more complicated data structure, such as a 2D array. With 2D arrays, the domain must be distributed evenly in both dimensions. In fact, to maximize efficiency, each processor’s domain is ideally a square, since this will minimize the ratio of border exchange to computation. The downside of this is that it can be difficult to partition the area up exactly.
When partitioning the problem domain, each process will only have access to a small portion (a local domain) of the global domain. Each process stores a local array and uses message passing to find the values of cells in neighboring processes, if necessary. Generally, it’s useful to work in global coordinates, in which case a global coordinate is provided to access some location of the parallel array, then the one processor that has that portion of the global array can send back a reference to the element. However, in this setup, only one process will be able to change a given element of the global array.
One problem with parallel grid structures is how to distribute the load evenly to all processors. For a $d$-dimensional grid with $N$ processors, the general strategy is to first decompose $N$ into $d$ factors. Then, along each dimension, the decomposed number of processors can divide the range of each dimension using a $1$-dimensional decomposition function. A simple numbering system can be used to assign each process to some part of the domain. See the figure below for an example of a $12 \times 18$ grid decompositioned by $6$ processors.
Often, it is necessary for a given grid element to get information about neighboring grid elements. (In cases where this is not necessary, the problem is known as “embarrassingly parallel”). However, in a distributed array, the edge of each process’ computational domain has cells that will not have direct access to some neighboring cells. To deal with this, a layer of ghost cells is added, so that after each iteration of a computation, the ghost cells are updated with the values of the would-be neighboring cells. This introduces a small amount of overhead that can become a major issue as the number of processors increases. See figure \ref{ghost_cell} for an example of ghost cell border exchange.
Message Passing Interface (MPI)
MPI is a framework for providing parallel implementations to programs. It uses a distributed memory parallel processing model, hence the “message passing.” MPI is one of the most standard ways of performing distributed memory parallel processing, and as such, comes standard in all DoD supercomputers. When MPI is implemented in a program, each of the $N$ processors runs through the same exact code. The only difference is that each processor is given a unique ID. This allows the program to explicitly divide the computational domain amongst the different processors.
I’ll stop there, because after that, I start getting into the actual details of my research. Anyway, the whole experience was fun and rewarding. One thing I really enjoyed was the actual programs I was working on. In order to benchmark the different frameworks, I had to have some test program, and for that I used an FDTD wave guide simulation. The only relevance of the program to my project was the fact that it involved a grid of “cells.” Despite that, it was fun coding the programs. You can see the result of one wave guide simulation after 709 steps (200.0 ms):
At the end of the NRL Internship, I had to create a Presentation to give to a group of students working in similar fields.
The next day, at the closing ceremony, they gave awards to the top two presentations in each group of students. I ended up getting 1st place in my group!
Overall, the whole experience was a lot of fun (even though it did occupy most of my summer). In fact, the mentors/post-docs were really nice. They took me bowling pretty much every week! I started off getting a score of around 55 per game (that’s really bad), but ended up getting near 100-120 (still bad, but not as bad).
Next year, I’ll be allowed to participate in a similar program, but with more flexible hours. That should be fun.